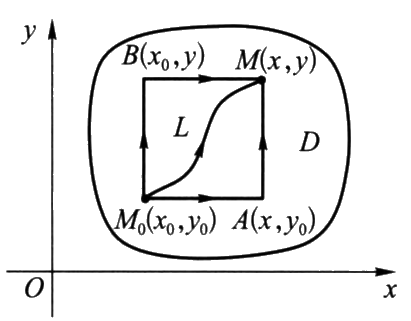第九章向量值函数的曲线积分与曲面积分

约 2586 个字 2 张图片预计阅读时间 9 分钟

向量值函数在有向曲线上的积分 ¶

向量场 ¶

若场中每一点对应的物理量是向量，则称该场为向量场。

若场中每一点对应的物理量是数量，则称该场为数量场。

若 $G$ 是一平面向量场，则可以用一个定义在 $G$ 上的二元向量值函数表示：

\[ \boldsymbol{\overrightarrow{F}}(x,y)=P(x,y)\boldsymbol{\overrightarrow{i}}+Q(x,y)\boldsymbol{\overrightarrow{j}} \]

若 $G$ 是一空间向量场，则可以用一个定义在 $G$ 上的三元向量值函数表示：

\[ \boldsymbol{\overrightarrow{A}}(x,y,z)=P(x,y,z)\boldsymbol{\overrightarrow{i}}+Q(x,y,z)\boldsymbol{\overrightarrow{j}}+R(x,y,z)\boldsymbol{\overrightarrow{k}} \]

向量线是位于向量场中这样的曲线：该曲线上每一点处的切线与该点的场向量重合。

向量场中的曲线有方向的概念。沿不同的方向积累的数值是相反的。我们规定非封闭曲线 $L$ 的两个端点 $A$ $B$ 有两个方向 $\stackrel\frown{AB}$ $\stackrel\frown{BA}$ 中的一个方向记为 $L$ 。另一个为 $L^-$ .

第二型曲线积分 ¶

定义：

设 $L$ 是空间中从点 $A$ 到点 $B$ 的一条有向光滑曲线段， $\boldsymbol{\overrightarrow{e_r}}$ 为 $L$ 上任一点 $(x,y,z)$ 处的单位切向量，其方向与 $L$ 的方向一致。在 $L$ 上定义一个向量值函数 $\boldsymbol{\overrightarrow{A}}(x,y,z)=P(x,y,z)\boldsymbol{\overrightarrow{i}}+Q(x,y,z)\boldsymbol{\overrightarrow{j}}+R(x,y,z)\boldsymbol{\overrightarrow{k}}$ , 其中 $P(x,y,z),Q(x,y,z),R(x,y,z)$ 在 $L$ 上有界，若数量积 $\boldsymbol{\overrightarrow{A}} \cdot \boldsymbol{\overrightarrow{e_r}}$ 在 $L$ 上的第一型曲线积分存在，则称此积分值为向量值函数 $\boldsymbol{\overrightarrow{A}}$ 在有向曲线段 $L$ 上的积分，或称第二型曲线积分。

\[ \int_L\boldsymbol{\overrightarrow{A}}\,\cdot\,\boldsymbol{\overrightarrow{e_r}}\,\mathrm{d}s \]

在直角坐标系中，记 $\boldsymbol{\overrightarrow{e_r}}=(\cos\alpha,\cos\beta,\cos\gamma)$ , 则有 $\boldsymbol{\overrightarrow{e_r}}\,\mathrm{d}s=(\mathrm{d}x,\mathrm{d}y,\mathrm{d}z)$ , 这时称 $\boldsymbol{\overrightarrow{e_r}}\,\mathrm{d}s$ 为有向弧微分，简写为 $\mathrm{d}\boldsymbol{\overrightarrow{s}}$ .

此时第二型曲线积分式子可以表示为：

\[ \int_L\boldsymbol{\overrightarrow{A}}\,\cdot\,\mathrm{d}\boldsymbol{\overrightarrow{s}}=\int_LP(x,y,z)\mathrm{d}x+Q(x,y,z)\mathrm{d}y+R(x,y,z)\mathrm{d}z \]

简记为

\[ \int_L\boldsymbol{\overrightarrow{A}}\,\cdot\,\mathrm{d}\boldsymbol{\overrightarrow{s}}=\int_LP\mathrm{d}x+Q\mathrm{d}y+R\mathrm{d}z \]

称为第二型曲线积分的坐标形式，因此也称第二型曲线积分为对坐标的曲线积分。

第二型曲线积分有线性性，可加性，有向性，都比较直观容易想象。

第二型曲线积分的计算 ¶

设空间有向光滑曲线段 $L$ 的参数方程为

\[ \left\{\begin{array}{l} x=x(t), \\ y=y(t), \\ z=z(t) \end{array}\right. \ \ (t:\alpha \to\beta) \]

则有第二型曲线计算公式：

\[ \int_LP\mathrm{d}x+Q\mathrm{d}y+R\mathrm{d}z=\int_\alpha^\beta\bigg[\,P(t)\,x'(t)+Q(t)\,y'(t)+R(t)\,z'(t)\,\bigg]\mathrm{d}t \]

Green 公式、平面曲线积分与路径无关的条件 ¶

平面区域有关概念 ¶

设 $D$ 为平面区域，如果 $D$ 内任意一条闭曲线所围部分都属于 $D$ ，则称 $D$ 为单连通区域；否则称 $D$ 为复连通区域．

直观上说，单连通区域不能有 “洞” .

平面区域 $D$ 有其边界曲线 $L$ , 规定 $L$ 的正向为：沿着正向行走时，区域 $D$ 总是在左边。即单连通区域的边界曲线 $L$ 的正向为逆时针方向，复连通区域的外边界曲线正向也是逆时针方向，而内边界曲线的正向为顺时针方向。

本节所讨论的闭曲线都是简单闭曲线，除了两个端点重合外，曲线自身不相交。

复联通区域可以通过划分转换为多个单连通区域。

格林公式 ¶

设平面闭区域 $D$ 是由分段光滑的闭曲线 $L$ 围成的单连通区域，函数 $P(x,y),Q(x,y)$ 上具有一阶连续偏导数，则有格林公式

\[ {\int \kern{-20mu} \bigcirc}_L\, P\, \mathrm{d}x +Q\,\mathrm{d}y=\iint_D\Big(\frac{\partial Q}{\partial x}-\frac{\partial P}{\partial y}\Big)\, \mathrm{d}x\mathrm{d}y. \]

由格林公式可以计算平面闭区域 $D$ 的面积：

\[ S=\iint_D\mathrm{d}x\mathrm{d}y=\frac{1}{2}{\int \kern{-20mu} \bigcirc}_L\Big(-y \,\mathrm{d}x+ x \,\mathrm{d}y\Big). \]

积分与路径无关的条件 ¶

设 $D$ 为平面上的单连通区域，函数 $P(x,y),Q(x,y)$ 上具有一阶连续偏导数，则下列四个命题等价：

1 对于 $D$ 内任何分段光滑的闭曲线 $L$ ，有

\[ {\int \kern{-20mu} \bigcirc}_L\, P\, \mathrm{d}x +Q\,\mathrm{d}y=0 \]

2 曲线积分 $\displaystyle{\int \kern{-20mu} \bigcirc}_L\, P\, \mathrm{d}x +Q\,\mathrm{d}y$ 的值在 $D$ 内与路径无关。

3 表达式 $P\, \mathrm{d}x +Q\,\mathrm{d}y$ 在 $D$ 内是某个二元函数 $u=(x,y)$ 的全微分，即

\[ \mathrm{d}u(x,y)=P\, \mathrm{d}x +Q\,\mathrm{d}y \]

4 等式在 $D$ 内处处成立 .

\[ \frac{\partial Q}{\partial x}=\frac{\partial P}{\partial y} \]

Info

此定理非常重要，它指出了平面上第二型曲线积分与路径无关的充要条件，也指出了表达式 $P\mathrm{d}x+Q\mathrm{d}y$ 是某个二元函数的全微分的充要条件．在这些充要条件中，命题 (4) 在使用中最为方便．

当曲线积分与路径无关时，对于较复杂的曲线积分，可以换一条便于计算的路径来计算．

原函数、全微分方程 ¶

根据前面的定理，若函数 $P(x,y),Q(x,y)$ 在单连通区域 $D$ 上具有一阶连续偏导数，且在 $D$ 内满足 $\frac{\partial Q}{\partial x}=\frac{\partial P}{\partial y}$ ，那么表达式 $P\, \mathrm{d}x +Q\,\mathrm{d}y$ 在 $D$ 内是某个二元函数 $u=(x,y)$ 的全微分，此时称 $u(x,y)$ 为 $P\, \mathrm{d}x +Q\,\mathrm{d}y$ 的一个原函数。$u(x,y)$ 可以由下面公式求得：

\[ u(x,y)=\int_{(x_0,y_0)}^{(x,y)} P\,\mathrm{d}x+Q\,\mathrm{d}y \]

这一过程被称为全微分求积。

因为此时积分与路径无关，因此可以选择简单的路径来计算积分，比如平直折线：

\[ \begin{gather} u(x,y)=\int_{x_0}^x P(x,y_0)\,\mathrm{d}x+\int_{y_0}^y Q(x,y)\,\mathrm{d}y \\ \\ u(x,y)=\int_{y_0}^y Q(x_0,y)\,\mathrm{d}y+\int_{x_0}^x P(x,y)\,\mathrm{d}x \end{gather} \]

如果一阶微分方程改写成

\[ P(x,y)\,\mathrm{d}x+Q(x,y)\,\mathrm{d}y=0 \]

后，其左端恰好满足上述等价关系，则这个方程为全微分方程。此时 $u(x,y)=C$ 是隐式通解，其中 $C$ 是任意常数。

总结平面第二类曲线积分 ¶

给出一个第二类曲线积分，如何求解？

第一步：判断函数整体是否满足

\[ \frac{\partial Q}{\partial x}\ {= \kern{-17mu} ^?}\ \frac{\partial P}{\partial y} \]

如果不相等，则用 Green 公式或直接设参数求定积分。

如果相等：

第二步：判断 $L$ 是否封闭

如果封闭，则利用积分与路径无关原则，重新选择路径计算

如果不封闭：

第三步：判断 $L$ 内部是否含有奇点（不满足第一公式）

如果没有奇点，直接 $=0$ .

如果有奇点，则只能用 Green 公式（挖去奇点，加辅助线）或设参数求定积分。

第二型曲面积分 ¶

定义：

设 $S$ 是空间中一有向光滑曲面， $\boldsymbol{\overrightarrow{n_0}}$ 为 $S$ 上任一点 $M(x,y,z)$ 处的单位法向量，其方向与 $S$ 的指定侧一致。在 $S$ 上定义一个向量值函数 $\boldsymbol{\overrightarrow{A}}(x,y,z)=P(x,y,z)\boldsymbol{\overrightarrow{i}}+Q(x,y,z)\boldsymbol{\overrightarrow{j}}+R(x,y,z)\boldsymbol{\overrightarrow{k}}$ , 其中 $P(x,y,z),Q(x,y,z),R(x,y,z)$ 在 $S$ 上有界，若数量积 $\boldsymbol{\overrightarrow{A}} \cdot \boldsymbol{\overrightarrow{n_0}}$ 在 $S$ 上的第一型曲面积分存在，则称此积分值为向量值函数 $\boldsymbol{\overrightarrow{A}}$ 在有向曲曲线 $S$ 上的积分，或称第二型曲面积分。

\[ \iint_L\boldsymbol{\overrightarrow{A}}\,\cdot\,\boldsymbol{\overrightarrow{n_0}}\,\mathrm{d}S \]

在直角坐标系中，记 $\boldsymbol{\overrightarrow{n_0}}=(\cos\alpha,\cos\beta,\cos\gamma)$ , 则有 $\boldsymbol{\overrightarrow{n_0}}\,\mathrm{d}S=(\mathrm{d}y\mathrm{d}z,\mathrm{d}z\mathrm{d}x,\mathrm{d}x\mathrm{d}y)$ , 这时称 $\boldsymbol{\overrightarrow{n_0}}\,\mathrm{d}S$ 为有向面积微元，简写为 $\mathrm{d}\boldsymbol{\overrightarrow{S}}$ .

此时第二型曲面积分式子可以表示为：

\[ \iint_L\boldsymbol{\overrightarrow{A}}\,\cdot\,\mathrm{d}\boldsymbol{\overrightarrow{S}}=\iint_LP(x,y,z)\mathrm{d}y\mathrm{d}z+Q(x,y,z)\mathrm{d}z\mathrm{d}x+R(x,y,z)\mathrm{d}x\mathrm{d}y \]

简记为

\[ \int_L\boldsymbol{\overrightarrow{A}}\,\cdot\,\mathrm{d}\boldsymbol{\overrightarrow{s}}=\int_LP\mathrm{d}y\mathrm{d}z+Q\mathrm{d}z\mathrm{d}x+R\mathrm{d}x\mathrm{d}y \]

称为第二型曲面积分的坐标形式，因此也称第二型曲面积分为对坐标的曲面积分。

第二型曲面积分有线性性，可加性，有向性，都比较直观容易想象。

第二型曲面积分的计算 ¶

设空间有向光滑曲线段 $S$ 的方程为

\[ z=z(x,y) \]

则有第二型曲线计算公式：

\[ \iint_L\boldsymbol{\overrightarrow{A}}\,\cdot\,\boldsymbol{\overrightarrow{n_0}}\,\mathrm{d}S=\pm\iint\limits_{D_{xy}}\boldsymbol{\overrightarrow{A}}\big(x,y,z(x,y)\big)\,\cdot\boldsymbol{\overrightarrow{n}}\,\mathrm{d}x\mathrm{d}y \]

其中 $\boldsymbol{\overrightarrow{n}}$ 取 $(-z_x,-z_y,1).$ $D_{xy}$ 是 $S$ 在 $Oxy$ 平面上的投影区域 . 当 $S$ 取上侧时为 $+$ ，取下侧时为 $-$ .

对于 $x=x(y,z)$ ，取右侧为 $+$ ；对于 $y=y(x,z)$ , 取前侧为 $+$ .

简便算法：设有向曲面 $S$ 的方程为 $z=z(x,y)$ , $S$ 在 $Oxy$ 平面上的投影区域为 $D_{xy}$ ，函数 $R(x,y,z)$ 在 $S$ 上连续，则有

\[ \iint\limits_{S}R(x,y,z)\,\mathrm{d}x\mathrm{d}y=\pm \iint\limits_{D_{xy}}R\big(\,x,y,z(x,y)\,\big)\,\mathrm{d}x\mathrm{d}y \]

当 $S$ 取上侧时为 $+$ , 当 $S$ 取下侧时为 $-$ .

$$ \iint\limits_{S}P(x,y,z)\,\mathrm{d}y\mathrm{d}z=\pm \iint\limits_{D_{yz}}P\big(\,x(y,z),y,z\,\big)\,\mathrm{d}y\mathrm{d}z $$ 当 $S$ 取前侧时为 $+$ , 当 $S$ 取后侧时为 $-$ .

\[ \iint\limits_{S}Q(x,y,z)\,\mathrm{d}z\mathrm{d}x=\pm \iint\limits_{D_{zx}}Q\big(\,x,y(z,x),z\,\big)\,\mathrm{d}z\mathrm{d}x \]

当 $S$ 取右侧时为 $+$ , 当 $S$ 取左侧时为 $-$ .

第九章 向量值函数的曲线积分与曲面积分